„Cînd ai doar un ciocan, toate obiectele din jur îți par cuie”. Așa sună prejudecata cognitivă numită legea instrumentului, atribuită psihologului american Abraham Maslow (1908-1970). Tendința de a te baza mai întîi pe ceea ce știi este naturală și pe ea se construiește orice experiență de învățare. Constați că te afli într-o situație nouă pentru care nu ești pregătit abia după ce epuizezi variantele deja cunoscute.

Dacă reușești, totuși, să obții ceva pe baza experienței, nu mai simți nevoia să înveți și ți se pare că știi deja răspunsul. De aceea, legea instrumentului este o prejudecată: îți dă impresia că știi ce ai de făcut doar pentru că ajungi la un rezultat.

Asta înseamnă o prejudecată: o convingere fermă că ai deja informația potrivită, fără să te mai gîndești dacă există alternative. Ai totul pre-judecat, ca și cum te-ai fi gîndit înainte și acum ai totul stabilit, numai bun de trecut la fapte.

Prejudecățile apar adesea în relațiile sociale, dar ele îți pot modela și modul în care te raportezi științific la lume. Poți avea prejudecăți care să-ți schimbe chiar felul în care înveți matematica.

Zgomotul vizual și iluziile optice

Un articol publicat de revista Science în iunie 2025 arată cum fondul cultural îți poate dicta felul în care vezi lucrurile, la propriu. Este cazul sătenilor comunității Himba, din Namibia (în imaginea de copertă), studiați de-a lungul anilor pentru mai multe particularități. În 2020, BBC scria despre vederea excelentă a acestor nomazi, dezvoltată de ocupația lor principală: creșterea vitelor, pe care le păstoresc în zone unde nu există prea multă vegetație și, în general, diversitate cromatică. De aceea, proprietarii vitelor le deosebesc prin semne colorate pe care le aplică pe animale, în nuanțe diferite, dar nu foarte stridente. Așa că acuitatea vizuală a comunității Himba este antrenată nu doar să urmărească vitele, dar și să identifice de la distanță semnele colorate ale turmelor.

Paradoxal, limba acestui popor nu conține cuvinte care să descrie toate nuanțele (fenomen cercetat și la nivel academic), însă vederea lor este cu mult mai dezvoltată decît a oamenilor crescuți la oraș sau în zone mai aglomerate.

Fenomenul a fost observat și la alte comunități rurale, care s-au dezvoltat departe de lumea aglomerată și civilizația modernă. Mai mult, migrația influențează aceste abilități. Nativii Himba care s-au mutat la oraș și-au pierdut acuitatea vizuală excepțională, pentru că stimulii urbani sînt mult mai mulți, iar creierul nu mai poate da atenție fiecăruia în parte. Așa că ajunge să facă doar o separare grosieră, un mecanism obișnuit de funcționare a atenției.

Dar mai important decît percepția rafinată a culorilor este reacția la iluzii optice. Într-un caz cunoscut cu linii de lungimi aparent diferite (numită iluzia Müller-Lyer), majoritatea oamenilor crescuți în comunități urbane moderne răspund greșit că liniile nu au aceeași lungime. Sîntem atît de obișnuiți cu liniile pe care le vedem la clădiri sau obiecte de mobilier, care ne-au învățat și cu iluzia perspectivei și cu alte relații geometrice reale sau aparente (perpendicularitate, paralelism, congruență ș.a.m.d.) încît mintea nu se mai poate concentra doar pe lungime.

Nomazii Himba, însă, au creierul mai liber de asemenea informații și, deci, de prejudecăți, așa că răspund mai des corect la astfel de provocări. La fel și alte comunități rurale, triburi și popoare migratoare trăite departe de zgomotul vizual al societății moderne.

Articolul din Science arată o distincție încă și mai fină, unde viața sătenilor Himba conduce la un rezultat surprinzător. Iluzia cufărului (eng. coffer), care își ia numele de la modelele care apar pe unele piese de mobilier, ascunde în tiparul rectangular mai multe cercuri. Majoritatea oamenilor crescuți și educați în comunități urbane moderne văd cu mare dificultate cercurile din acest tipar. Nu și etnicii Himba, pentru care situația stă exact invers: ei văd cu ușurință cercurile și trebuie instruiți ca să se poată concentra asupra dreptunghiurilor.

Explicația vine din stilul lor de viață și organizare rurală. Etnicii Himba își construiesc colibe circulare (aproape emisferice, ca niște igluuri din pămînt și paie), pentru că au o viață de nomazi și nu au nevoie de locuințe durabile. Ei mai construiesc țarcuri circulare pentru vite, iar în jurul comunității ridică un fel de gard, astfel că micile sate au cu totul un aspect circular. De aici prejudecata către obiecte circulare, față de clădirile pline de unghiuri pe care le conțin orașele moderne.

Numerele ca produs cultural

În spatele percepției vizuale a cercurilor sau a dreptunghiurilor din iluzia cufărului se află informația geometrică abstractă. Nativii Himba au putut face trecerea de la forma rotundă a colibelor la cercuri într-o imagine, deci înclinația lor spre forma circulară este generală, abstractizată din formele obiectelor cu care sînt obișnuiți. Prejudecata apare la nivel profund, abstract, nu doar în ce privește colibele sau gardurile.

În 1981, matematicianul și istoricul Raymond Wilder a publicat cartea Mathematics as a Cultural System. Autorul argumentează că evoluția în general este un produs cultural, în sensul că oamenii, dar și celelalte viețuitoare, precum și obiectele pe care le produc — inclusiv obiecte ale gîndirii, ca matematica sau descoperirile științifice — se dezvoltă strîns legat de cultura căreia aparțin. Unul dintre cele mai importante elemente culturale este limbajul și, conform exemplelor lui John D. Barrow și studiilor lui George Lakoff despre care am scris într-un articol anterior, vocabularul și întregul fond lingvistic al unui popor îi influențează evoluția, inclusiv din punctul de vedere al percepției și dezvoltării științelor și matematicii.

Dacă ar fi vorba doar despre limbaj, însă, am fi numit matematica produs lingvistic, nu cultural. Dar într-un studiu din 2008, cercetătorii francezi Stanislas Dehaene și Véronique Izard arată că elementele culturale influențează percepția asupra direcției axelor numerice, lucru care nu se leagă de abilitățile lingvistice.

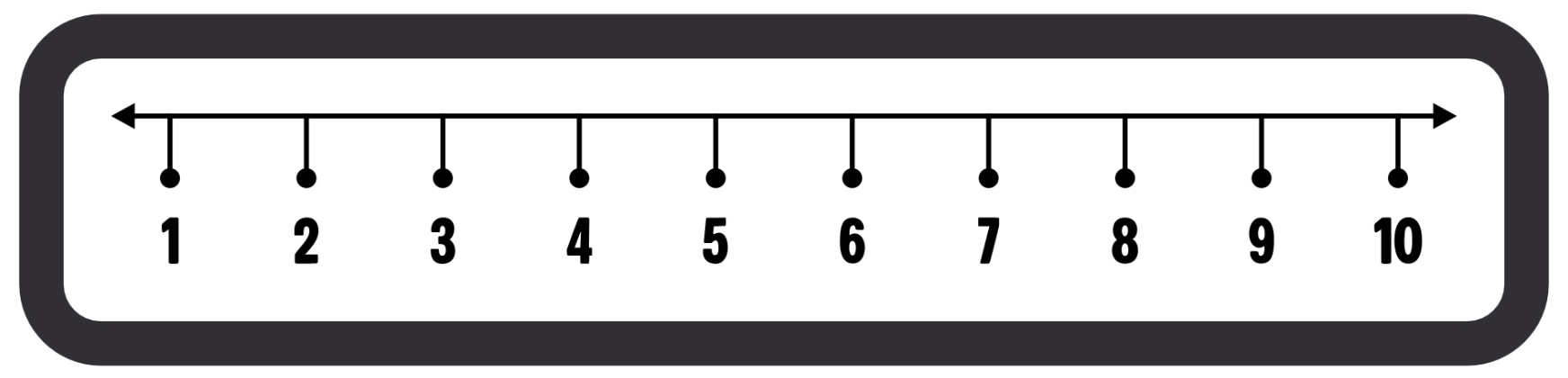
Axa numerelor reale le ordonează crescător de la stînga la dreapta, cu „punctul de la infinit” aflat la extrema dreaptă, iar „minus infinitul” aflat la extrema stîngă. Dar și acesta este un produs cultural, arată Dehaene și Izard. Cei doi au cooptat studenți din țări arabe și din țări europene, cărora li s-au prezentat numere în succesiune. Cînd numărul curent era mai mare decît anteriorul, semnalau printr-un buton care indică dreapta — ordinea crescătoare a numerelor de pe axă.

Studenții din țări arabe au avut dificultăți mult mai mari decît participanții europeni și au plasat mai des numerele mai mari la stînga predecesorilor. Mai mult, s-a putut vedea cum studenții naturalizați, adică născuți în țări arabe, dar mutați în Franța sau în alte țări europene, răspundeau asemănător nativilor europeni. Factorul cultural — aici, direcția de scriere — ajungea să-și piardă influența asupra răspunsului la experiment după aproximativ zece ani. Studenții arabi care locuiau de aproape un deceniu în țări europene au avut rezultate foarte asemănătoare cu nativii europeni.

Educație sau natură matematică

Încadrarea unor abilități matematice sub influența fondului cultural deschide o altă discuție, mult mai amplă: aceea despre natură și educație (mai cunoscută sub denumirea din engleză, nature vs. nurture). Exemplele de pînă acum ar justifica implicarea semnificativă a educației, a creșterii și dezvoltării în sensul general (nurture) în abilități de tip matematic (geometric sau aritmetic).

De cealaltă parte, experimente precum cel al lui E. L. Kaufman din 1949 sau al lui Karen Wynn din 1992 arată că există un bagaj fundamental de natură matematică — mai bine zis, aritmetică — în fiecare dintre noi, care se manifestă din primele luni de viață, cu mult înainte ca elementele culturale să aibă vreo influență.

Studiul lui Kaufman arată că avem o abilitate de a „număra instantaneu” maximum șase obiecte, abilitate pe care a numit-o subitizare, pentru a evidenția caracterul subit. Participanții s-au uitat la ecrane pe care se proiectau numere diverse de puncte pentru o durată mult mai mică decît ar fi fost necesară numărării conștiente (sub 300 milisecunde). Apoi, aveau de notat numărul de puncte pe care l-au văzut. Rezultatul a fost că, atunci cînd se proiectaseră cel mult șase puncte, acuratețea era aproape maximă.

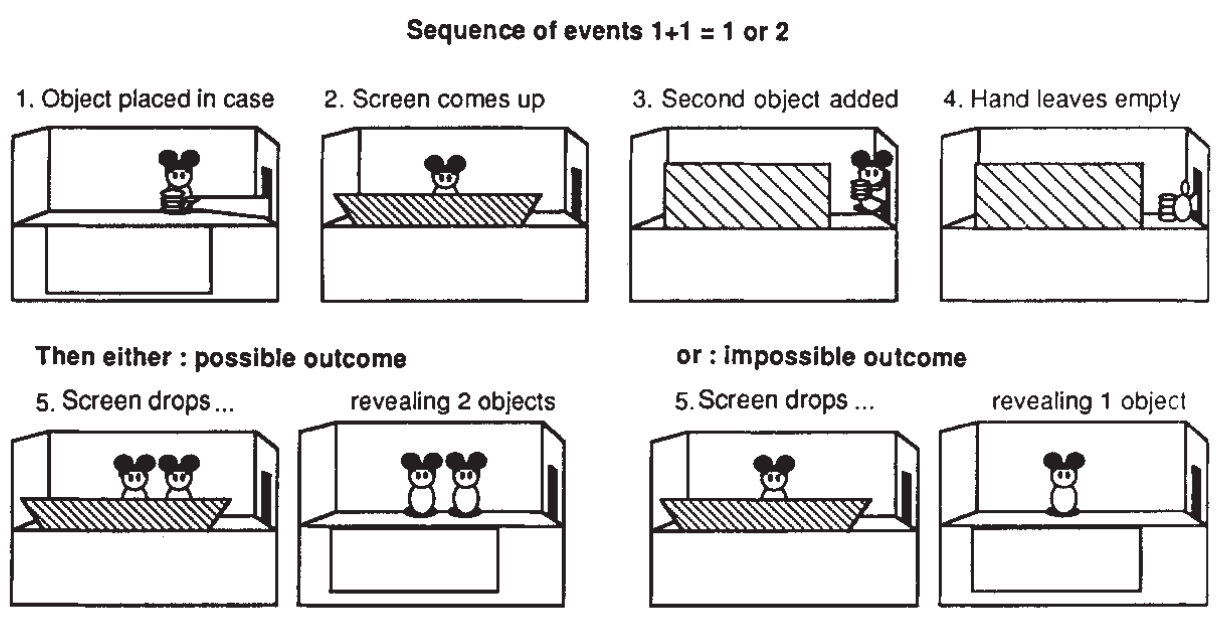
Karen Wynn a folosit un fel de teatru de păpuși prin care să sugereze operații aritmetice elementare. Copii cu vîrsta de maximum cinci luni veneau și urmăreau un teatru de păpuși improvizat, cu o singură păpușă. La căderea cortinei, se mai introducea încă o păpușă, pentru ca la ridicarea ei, pe scenă să fie în unele cazuri una, în altele două păpuși. Pentru situația aritmetic imposibilă (1 + 1 = 1), copiii se uitau curioși, mult mai nedumeriți decît în situația corectă (1 + 1 = 2).

Dehaene însuși a scris o carte, The Number Sense (1996, reeditată în 2011), în care arată că există un fel de simț primitiv al numărului în creierul uman, dar și al unor animale. Și nu este singurul exemplu: matematicianul Keith Devlin a publicat și el o carte similară, în 2009, cu titlul The Math Instinct: Why You’re a Mathematical Genius (Along with Lobsters, Birds, Cats, and Dogs).

Este abstractizarea o prejudecată?

În ansamblu, cred că situația prezintă nuanțe. Mai întîi, e clar că abilitatea de a număra pînă la maximum 6, de a înțelege intuitiv că 1 + 1 = 2 sau de a distinge între cercuri și dreptunghiuri nu înseamnă „matematică”. Totuși, în spatele acestor sarcini simple se află o capacitate de abstractizare foarte importantă pentru orice matematician, indiferent de nivel.

Majoritatea sistemelor de educație pornesc de la exemple concrete, de multe ori preluate din cotidian, pentru ca apoi să abstractizeze. Dau doar exemplul rezolvării problemelor prin metoda grafică, introdusă în clasele primare. Treptat, ea este înlocuită cu problemele „cu text” din care elevul extrage informațiile matematice, pe care apoi le formulează ca ecuații și le rezolvă, independent aproape de contextul inițial. De fapt, așa s-a construit întreaga cunoaștere matematică sau științifică: prin abstractizarea situațiilor concrete.

De aceea, capacitatea prin care nativii Himba leagă forma colibelor de cercurile de pe hîrtie sau ecran sau lejeritatea prin care copiii de patru luni înțeleg că o păpușă înseamnă 1 nu îi face matematicieni, dar arată că au abilități de abstractizare, esențiale nu doar în matematică.

Cît despre dezbaterea dintre natură și educație, văd argumente pentru capacități înnăscute rudimentare, modelate ulterior de cultură, educație și evoluție. Dar matematica și științele transcend cultura, căci istoria a evidențiat cercetători străluciți în mai toate popoarele și culturile lumii. Accesul la educație este și el un factor hotărîtor, ca și apartenența la o comunitate științifică, însă toate acestea se construiesc pe un fond ale cărui rădăcini sînt chiar abilitățile de abstractizare a formelor geometrice sau a numerelor și aritmeticii din obiecte înconjurătoare.

În fine, cred că prejudecata cognitivă din legea instrumentului nu este neapărat un dezavantaj. De multe ori, prejudecățile au conotații negative, fiindcă în mintea în care apar, realitatea este distorsionată încît să se conformeze modelului pe care îl creează. Dar baza prejudecăților se poate și rafina pînă cînd ajunge mai degrabă o înclinație, mai apropiată de o specializare decît de o legătură compromisă cu realitatea. Astfel, „simțul abstractului”, chiar cu nuanțe culturale pronunțate, devine un avantaj, nu un defect.